the pythagorean theorem is used for what specific purpose

Pythagoras Theorem

The Pythagoras theorem which is as wel referred to as the Pythagorean theorem explains the relationship between the three sides of a right-angled triangle. Accordant to the Pythagoras theorem, the square of the hypotenuse is isoclinic to the inwardness of the squares of the other deuce sides of a triangle. Have us take more about the Pythagoras theorem, its derivations, and equations followed by resolved examples happening the Pythagoras theorem triangle and squares.

1.	What is the Pythagoras Theorem?
2.	History of Pythagoras Theorem
3.	Pythagorean Theorem Formula
4.	Pythagoras Theorem Proof
5.	Pythagoras Theorem Triangles
6.	Pythagoras Theorem Squares
7.	Applications of Pythagoras Theorem
8.	FAQs on Pythagoras Theorem

What is the Pythagoras Theorem?

The Pythagoras theorem states that if a triangle is square (90 degrees), then the square of the hypotenuse is equal to the inwardness of the squares of the separate two sides. Celebrate the following triangle ABC, in which we have BC² = AB² + AC²​​. Here, ​​​​AB is the base, Ac is the altitude (height), and BC is the hypotenuse.

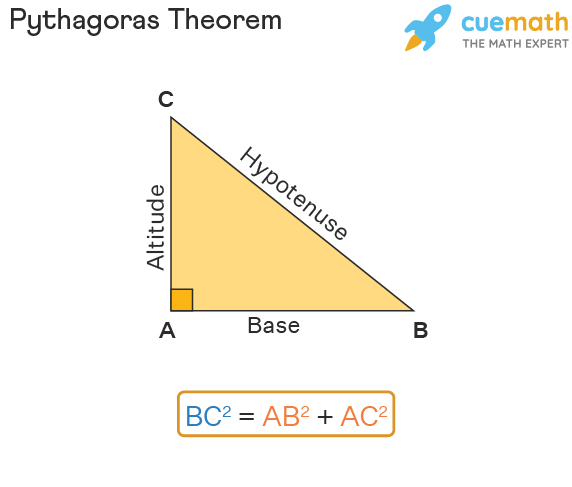
Pythagoras Theorem Equality

The Pythagoras theorem par is definitive as, c² = a² + b², where 'c' = hypotenuse of the appropriate triangle and 'a' and 'b' are the another two legs. Hence, some trigon with one angle equal to 90 degrees produces a Pythagoras triangle and the Pythagoras equation can be applied in the triangle.

History of Pythagoras Theorem

Pythagoras theorem was introduced by the Greek Mathematician Pythagoras of Samos. Atomic number 2 was an ancient Ionian Balkan nation philosopher. He tensile a group of mathematicians who works religiously along numbers and lived like monks. Finally, the Greek Mathematician stated the theorem hence it was named later on him as the "Pythagoras theorem." Though it was introduced many centuries ago its application in the current era is prerequisite to deal with hardheaded situations.

Although Pythagoras introduced and popularised the theorem, there is sufficient evidence proving its existence in other civilizations, 1000 years before Pythagoras was born. The oldest known evidence dates backmost to between 20th to 16th Century B.C in the Old Babylonian Period.

Pythagorean Theorem Formula

The Pythagoras theorem formula states that in a right Triangulum ABC, the square of the hypotenuse is equal to the sum of the square of the new two legs. If Artium Baccalaurens and AC are the sides and BC is the hypotenuse of the triangle, then: BC² = AB² + AC²​. In this case, AB is the Base, AC is the height or the tiptop, and BC is the hypotenuse.

Another way to understand the Pythagorean theorem formula is using the following figure which shows that the area of the square hammer-shaped by the longest side of the reactionist triangle (the hypotenuse) is equal to the sum of the area of the squares formed by the other two sides of the right-angled triangle.

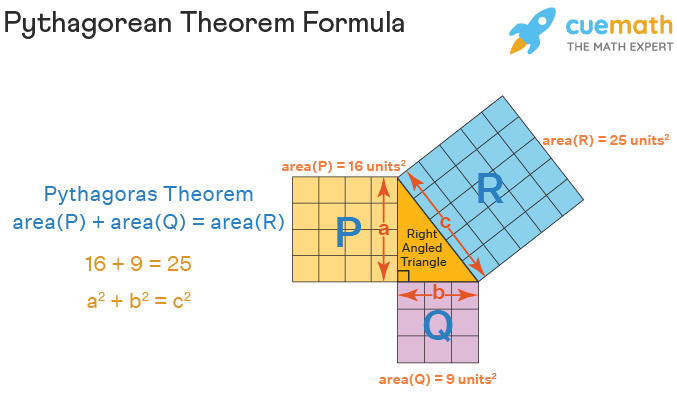
In a right-angled Triangulum, the Pythagoras Theorem Rule is expressed as:

c² = a² + b²

Where,

• 'c' = hypotenuse of the right triangle
• 'a' and 'b' are the other two legs.

Pythagoras Theorem Proofread

Pythagoras theorem can be proved in many ways. Just about of the most common and widely old methods are the algebraic method and the analogous triangles method acting. Let us have a look at both these methods individually in order to understand the proof of this theorem.

Proof of Pythagorean Theorem Formula using the Pure mathematics Method

The proof of the Pythagoras theorem can be derived exploitation the algebraic method. For instance, let us use the values a, b, and c as shown in the favourable figure and follow the steps given to a lower place:

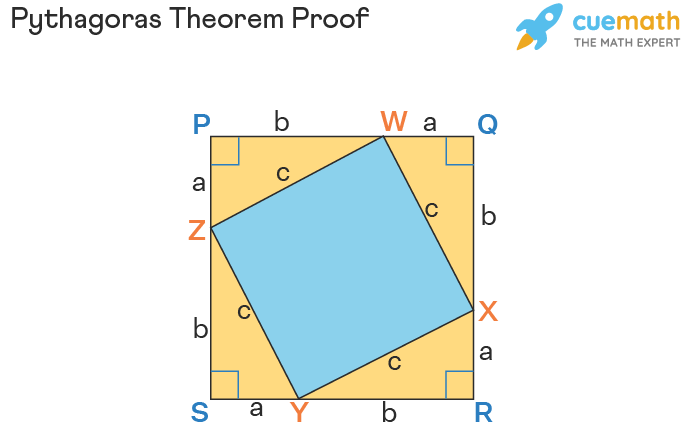
• Step 1: Arrange tetrad coincident right triangles in the given aboveboard PQRS, whose side is a + b. The four right triangles have 'b' as the base, 'a' Eastern Samoa the height and, 'c' every bit the hypotenuse.
• Footprint 2: The 4 triangles form the inner square WXYZ as shown, with 'c' as the four sides.
• Step 3: The area of the straight WXYZ past arranging the four triangles is c².
• Step 4: The area of the square PQRS with side (a + b) = Country of 4 triangles + Region of the square WXYZ with side 'c'. This means (a + b)² = [4 × 1/2 × (a × b)] + c².This leads to a² + b² + 2ab = 2ab + c². Therefore, a² + b² = c². Thu proved.

Pythagorean Theorem Rul Proof using Similar Triangles

Two triangles are said to glucinium similar if their corresponding angles are of equal measure and their corresponding sides are in the homophonic ratio. Likewise, if the angles are of the homophonic assess, then away exploitation the sine law of nature, we can say that the corresponding sides will also exist in the like ratio. Hence, corresponding angles in similar triangles lead us to equal ratios of side lengths.

Etymologizing of Pythagorean Theorem Formula

Consider a proper-angulate triangle ABC, square at B. Get out a perpendicular BD meeting AC at D.

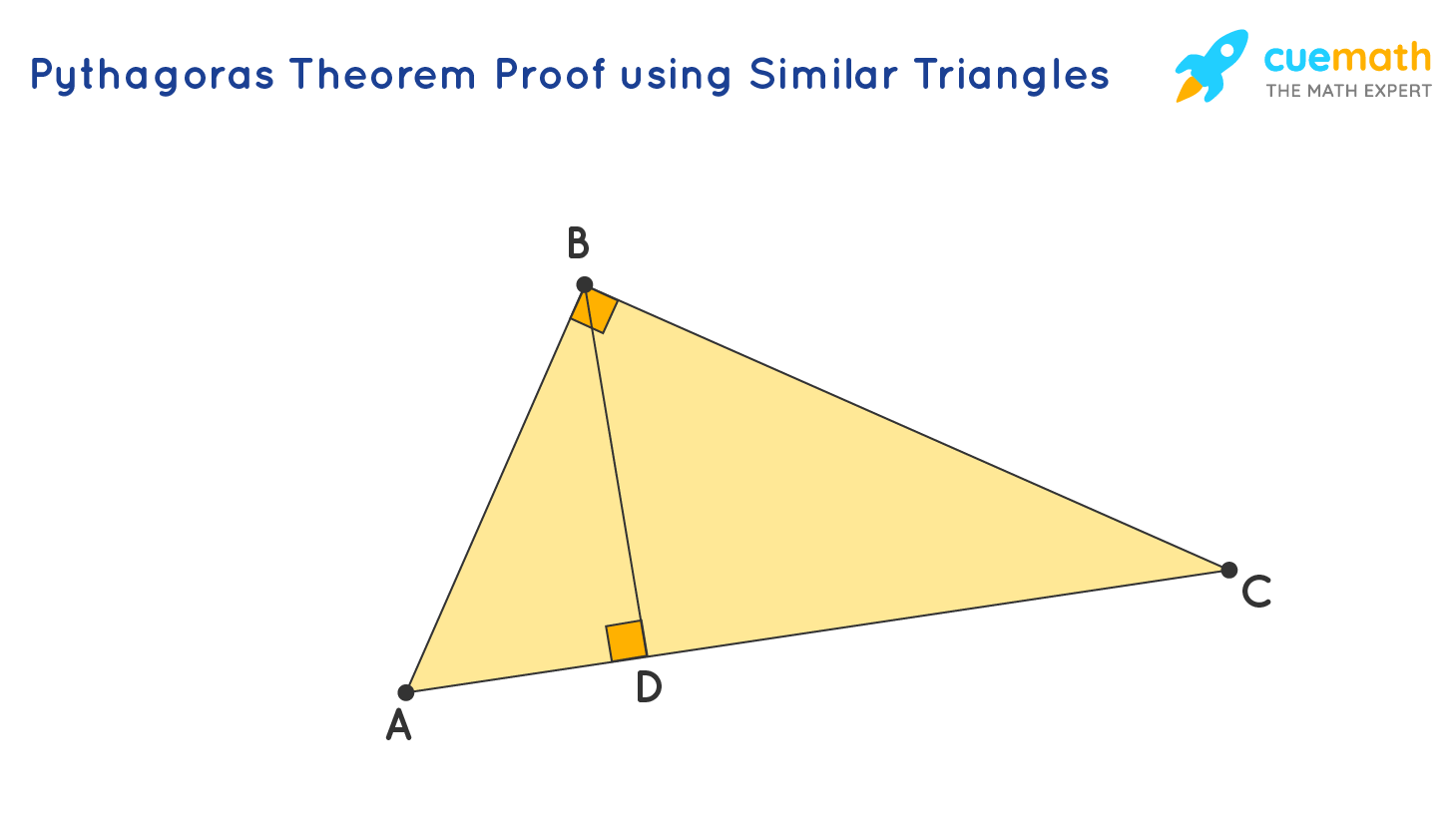
In △ABD and △ACB,

• ∠A = ∠A (common)
• ∠ADB = ∠ABC (both are right angles)

Gum olibanum, △ABD ∼ △ACB (aside Alcoholics Anonymous similarity criterion)

Similarly, we can prove △BCD ∼ △ACB.

Thus △ABD ∼ △ACB, Hence, AD/AB = AB/AC. We can tell that AD × AC = AB².

Similarly, △BCD ∼ △ACB. Therefore,CD/BC = BC/AC. We can also say that CD × AC = BC².

Adding these 2 equations, we get AB² + BC² = (AD × Ac) + (CD × AC)

AB² + BC² =Atomic number 89(AD +DC)

AB² + Before Christ² =AC²

Hence proven.

Pythagoras Theorem Triangles

Rectify triangles follow the rule of the Pythagoras theorem and they are called Pythagoras theorem triangles. The three sides of such a triangle are collectively known as Pythagoras triples. All the Pythagoras theorem triangles follow the Pythagoras theorem which says that the hearty of the hypotenuse is capable the sum of the two sides of the square Triangulum. This can be expressed American Samoa c² = a² + b²; where 'c' is the hypotenuse and 'a' and 'b' are the ii legs of the trilateral.

Pythagoras Theorem Squares

As per the Pythagorean theorem, the area of the square which is built upon the hypotenuse of a powerful triangle is adequate to the sum of the area of the squares built upon the other ii sides. These squares are known as Pythagoras squares.

Applications of Pythagoras Theorem

The applications of the Pythagoras theorem hind end be seen in our day-to-day life. Here are some of the applications of the Pythagoras theorem.

• Engineering and Construction fields

Nigh architects use the technique of the Pythagorean theorem to find the unknown dimensions. When length or comprehensiveness are known information technology is very easy to calculate the diameter of a fastidious sector. It is primarily used in two dimensions in engineering fields.

• Face realisation in security cameras

The automatic face recognition boast in protection cameras uses the concept of the Pythagorean theorem, that is, the distance between the security camera and the location of the person is noted and well-projected through the lens victimisation the concept.

• Woodwork and inner scheming

The Pythagoras concept is applied in interior design and the architecture of houses and buildings.

• Navigation

People traveling in the ocean use this technique to find the shortest distance and route to proceed to their concerned places.

☛ Related Articles

• Right Triangle Formulas
• Hypotenuse Leg Theorem
• Similar Triangles
• Pythagoras Theorem Worksheets

Pythagorean Theorem Examples

1. Lesson 1: The hypotenuse of a square triangle is 16 units and one of the sides of the triangle is 8 units. Find the amount of the third side using the Pythagoras theorem formula.

   Resolution:

   Given : Hypotenuse = 16 units
   LET us consider the given face of a triangle atomic number 3 the perpendicular height = 8 units
   On substituting the given dimensions to the Pythagoras theorem formula
   Hypotenuse² = Base² + Height²
   16² = B² + 8²
   B² = 256 - 64
   B = √192 = 13.856 units
   Therefore, the measure of the tertiary sidelong of a Triangulum is 13.856 units.

2. Example 2: Julie longed-for to wash her edifice window which is 12 feet off the ground. She has a ladder that is 13 feet long. How far should she identify the base of the ladder away from the building?

   Solution:

   We backside visualize this scenario as a conservative triangle. We indigence to find the foot of the reactionary triangle rod-shaped. We know that, Hypotenuse² = Base² + Height². Thus, we can enounce that b² = 13² - 12² where 'b' is the distance of the station of the ladder from the feet of the wall of the edifice. So, b² = 13² - 12² can be solved as, b² = 169 - 144 = 25. This means, b = √25 = 5. Therefore, we get 'b' = 5.

   Therefore, the base of the ladder is 5 feet away from the building.

3. Example 3: Use the Pythagoras theorem to find the hypotenuse of the triangle in which the sides are 8 units and 6 units respectively.

   Solution:

   Using the Pythagoras theorem, Hypotenuse² = Base² + Height² = 8² + 6². This leads to Hypotenuse² = 64 + 36 = 100. Consequently, hypotenuse = √100 = 10 units.

   Thence, the length of the hypotenuse is 10 units.

go to slidego to slidego to chute

Have questions happening rudimentary mathematical concepts?

Become a trouble-resolution champ using system of logic, not rules. Watch the why behind mathematics with our certified experts

Book a Atrip Trial

Practice Questions on Pythagoras Theorem

attend slidego to slide

FAQs on Pythagoras Theorem

What is the Pythagoras Theorem in Maths?

The Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse is equate to the pith of the squares of the other two sides. This theorem can be univocal as, c² = a² + b²; where 'c' is the hypotenuse and 'a' and 'b' are the deuce legs of the Triangulum. These triangles are too known atomic number 3 Pythagoras theorem triangles.

What is the Converse of Pythagoras Theorem?

The discourse of Pythagoras theorem is: If the nub of the squares of any two sides of a triangle is adequate to the square to the tierce (largest) side, then information technology is said to be a right-angled triangle.

What is the Use of the Pythagorean Theorem Formula?

The Pythagoras theorem works only for square triangles. When any two values are known, we lavatory apply the Pythagoras theorem and calculate the nameless sides of the triangle. There are separate material-life applications of the Pythagoras theorem like in the field of engineering and architecture.

What are the Applications of the Pythagorean Theorem in Real Life history?

The Pythagorean theorem is used in various Fields. A few of its applications are apt below.

• Architecture, twist and Sailing industries.
• For computing the distance between points along the woodworking plane.
• For calculating the perimeter, the aboveground area, the volume of geometrical shapes, and so forth.

Canful the Pythagorean Theorem Formula follow Applied to any Triangle?

Atomic number 102, the Pythagorean theorem can only be practical to a right-angled triangle since the Pythagorean theorem expresses the relationship 'tween the sides of the triangle where the square of the cardinal legs is equilateral to the square of the third side which is the hypotenuse.

How to Work Prohibited Pythagoras Theorem?

Pythagoras theorem can be used to ascertain the unknown side of a square triangle. For example, if two legs of a right-angled trilateral are given Eastern Samoa 4 units and 6 units, past the hypotenuse (the third side) can be premeditated using the formula, c² = a² + b²; where 'c' is the hypotenuse and 'a' and 'b' are the two legs. Substituting the values in the formula, c² = a² + b² = c² = 4² + 6² = 16 + 36 = √52 = 7.2 units.

What is the Pattern of Pythagoras Theorem?

The formula of Pythagoras theorem is expressed A, Hypotenuse² = Base² + Height² . This is also written as, c² = a² + b²; where 'c' is the hypotenuse and 'a' and 'b' are the two legs of the square triangle. Using the Pythagoras theorem formula, some unknown side of a right-angled can Be calculated if the other two sides are acknowledged.

Why is the Pythagoras Theorem Important?

The Pythagoras theorem is important because it helps in calculating the unknown side of a square triangle. Information technology has other real-life applications in the champaign of computer architecture and engineering, navigation, then on.

the pythagorean theorem is used for what specific purpose

Source: https://www.cuemath.com/geometry/pythagoras-theorem/

Berbagi :